Páginas
"Ensinar é um exercício de imortalidade . De alguma forma continuaremos a viver naqueles, cujos olhos aprenderam a ver o mundo pela magia de nossas palavras. O professor, assim não morre jamais."
Pesquisar este blog
Marcadores
- 1º Ano - Ensino Médio (3)
- 2º Ano - Ensino Médio (3)
- 8º ano (9)
- 9º ano (11)
- Aulas (13)
- Curiosidades (12)
- Cursos (4)
- Datas (1)
- Desafios (1)
- Dicas e Macetes (12)
- Downloads (1)
- Enem (2)
- Enigmas (3)
- Exercícios (3)
- Filmes (2)
- Física (5)
- Humor (5)
- Livros para Download (3)
- Matemática (17)
- Matemática Divertida (7)
- Mensagens aos Alunos (1)
- Provas (1)
- Química (9)
- Química divertida (2)
- Respostas dos Desafios (1)
- Tangran (2)
- Top Sites (1)
- Video Aulas (5)
- Vídeos (1)
Seguidores
Jackson Cabballero Rios Dória. Tecnologia do Blogger.
Arquivo do blog
Total de visualizações de página
Quem sou eu

- Loyxx Downloads
- Existem muitos blogs circulando pela nossa aldeia. Os que mais se destacam são aqueles que trazem sempre em primeira mão as grandes novidades que rola pelo mundo. Este, definitivamente, será o blog das novidades!
You can replace this text by going to "Layout" and then "Page Elements" section. Edit " About "
Mostrando postagens com marcador Aulas. Mostrar todas as postagens
Mostrando postagens com marcador Aulas. Mostrar todas as postagens
Você está em: Home » Artigos do Marcador Aulas
Desvendando a Física - Aceleração Média
Aceleração média
Quando um movimento apresenta variação da sua velocidade, ao longo do tempo, o movimento é um movimento variado - apresenta aceleração.
Quando um movimento apresenta variação da sua velocidade, ao longo do tempo, o movimento é um movimento variado - apresenta aceleração.
Os movimentos acelerados apresentam um aumento da velocidade e os retardados uma diminuição da velocidade.
A aceleração é uma grandeza que indica como a velocidade de um corpo varia ao longo do tempo.
A aceleração média,
em que 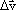 é a variação da velocidade no intervalo de tempo Dt.
é a variação da velocidade no intervalo de tempo Dt.
A aceleração é uma grandeza vectorial, que tem a mesma direcção do vector velocidade,
A unidade S.I. da aceleração é o m.s-2.
Aceleração instantâneaA aceleração instantânea é o valor da aceleração de um corpo num determinado instante.
Movimento rectilíneo uniformemente acelerado (m.r.u.a.)É um movimento em linha recta, com um valor de aceleração constante positivo (Gráfico 1). O valor da velocidade do corpo aumenta ao longo do tempo (Gráfico 2). A aceleração 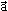 , tem a mesma direcção e o mesmo sentido da velocidade,
, tem a mesma direcção e o mesmo sentido da velocidade, 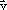 .
.
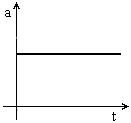 Gráfico 1 | 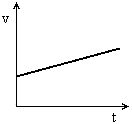 Gráfico 2 |
Movimento rectilíneo uniformemente retardado (m.r.u.r.)
É um movimento em linha recta, com um valor de aceleração constante negativo (Gráfico 3). A velocidade diminui ao longo do tempo (Gráfico 4). A aceleração,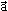 , tem a mesma direcção e sentido inverso ao da velocidade,
, tem a mesma direcção e sentido inverso ao da velocidade, 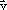 .
.
É um movimento em linha recta, com um valor de aceleração constante negativo (Gráfico 3). A velocidade diminui ao longo do tempo (Gráfico 4). A aceleração,
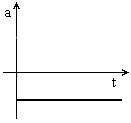 Gráfico 3 | 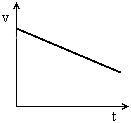 Gráfico 4 |
Desvendando a Química - Família dos Elementos - Metais Alcalinos
Metais Alcalinos
 Os Alcalinos são os elementos do Grupo 1 (1A) da Tabela Periódica, constituindo uma família ou uma série química. Formada pelos seguintes metais: lítio (Li), sódio (Na), potássio (K), rubídio (Rb), césio (Cs) e frâncio (Fr).
Os Alcalinos são os elementos do Grupo 1 (1A) da Tabela Periódica, constituindo uma família ou uma série química. Formada pelos seguintes metais: lítio (Li), sódio (Na), potássio (K), rubídio (Rb), césio (Cs) e frâncio (Fr).Têm este nome porque reagem muito facilmente com a água e, quando isso ocorre, formam hidróxidos (substâncias básicas ou alcalinas), libertando hidrogênio. Estes metais também reagem facilmente com o oxigênio produzindo óxidos.
Equação química da reação de um metal alcalino (exemplo: lítio) com a água:
2 Li(s) + 2 H2O(l) ===> 2 LiOH(aq) + H2(g)
Equação química da reação de um metal alcalino (exemplo: potássio) com o oxigênio:
4 K(s) + O2(g) ===> 2 K2O(s)
São metais de baixa densidade, coloridos e moles. Altamente eletropositivos e reativos. A eletropositividade e a reatividade destes elementos tende a crescer, no grupo, de cima para baixo se visto do ponto de vista termodinâmico (liberação de energia), pois quanto menor, mais o elemento se hidrata, oxidando mais rápido e reagindo mais rápido, se visto do ponto de vista cinético (velocidade da reação) a reatividade tende a crescer de baixo para cima, pois quanto maior os átomos mais fácil de perder o seu elétron de valência e mais rápido reage. Apresentam um único elétron nos seus níveis de energia mais externos (em subnível s), tendendo a perdê-lo, transformando-se em íons monopositivos: M+.
O hidrogênio, com um único elétron, está situado normalmente na tabela periódica no mesmo grupo dos metais alcalinos (ainda que às vezes apareça separado destes em outra posição). Porém, a energia necessária para arrancar o elétron do hidrogênio é muito mais elevada do que a qualquer alcalino. Como nos halogênios o hidrogênio necessita receber um único elétron para completar o seu nível mais externo. Na sua forma elementar é encontrado como uma molécula diatômica, H2. Pode formar sais denominados hidretos (MH) com os alcalinos, de forma que o metal cede um elétron ao hidrogênio, como se o hidrogênio fosse um halogênio. Devido à peculiaridade do hidrogênio prefere-se não classificar o hidrogênio em nenhuma série química.
Desvendando a Química - Distribuição Eletrônica
O diagrama de Linus Pauling é um diagrama elaborado pelo químico norte-americano Linus Carl Pauling para auxiliar na distribuição dos elétrons pelos subníveis da eletrosfera. A eletrosfera é a região externa do átomo onde se localizam os elétrons.
A eletrosfera é dividida em sete camadas que recebem letras do alfabeto (K, L, M, N, O, P e Q) de acordo com a distância que há entre ela e o núcleo. São escritas em letras maiúsculas.
Em 1913, o físico dinamarquês Niels Böhr, baseando-se em trabalhos anteriores, propôs que os elétrons giravam ao redor do núcleo do átomo em camadas eletrônicas ou níveis de energia. Também afirmou que estes elétrons não ganham nem perdem energia ao movimentar-se em sua camada. Porém, os elétrons de um átomo podem ganhar energia e saltar para uma camada mais externa. Assim, este átomo passa a ter seus elétrons em estado excitado. Quando os elétrons voltam para sua camada original, liberam a energia adquirida anteriormente na forma de fótons.
Cada camada da eletrosfera é dividida em subníveis. Os subníveis são designados por letras minúsculas: s (sharp = nítido), p (principal), d (diffuse = difuso), f (fundamental), g, h e i, sendo esses 3 últimos ausentes no diagrama convencional, pois apesar de existirem na teoria, não há átomo que possua tantos elétrons e que seja necessário utilizar esses subníveis.
Cada camada da eletrosfera é dividida em subníveis:
· A camada K é composta pelo subnível s.
· A camada L é composta pelos subníveis s e p.
· A camada M é composta pelos subníveis s, p e d.
· A camada N é composta pelos subníveis s, p, d e f.
· A camada O é composta pelos subníveis s, p, d, f e g.
· A camada P é composta pelos subníveis s, p, d, f, g, e h.
· A camada Q é composta pelos subníveis s, p, d, f, g, h e i
Os subníveis suportam no máximo:
· s - 2 elétrons.
· p - 6 elétrons.
· d - 10 elétrons.
· f - 14 elétrons.
· g - 18 elétrons.
· h - 22 elétrons.
· i - 26 elétrons.
Assim, a camada K, que só possui o subnível s, apresenta no máximo 2 elétrons. Já a camada L, que possui os subníveis s e p, apresenta no máximo 8 elétrons (2 provenientes do subnível s e 6 provenientes do subnível p) e assim sucessivamente.
Camada de valência é o último nível de uma distribuição eletrônica. Normalmente os elétrons pertencentes à camada de valência, são os que participam de alguma ligação química, pois são os mais externos. A contagem e distribuição dos elétrons é feita sempre de dentro (perto do núcleo) para fora.
Linus Carl Pauling, químico americano, elaborou um dispositivo prático que permite colocar todos os subníveis de energia conhecidos em ordem crescente de energia. É o processo das diagonais, denominado diagrama de Pauling, representado a seguir. A ordem crescente de energia dos subníveis é a ordem na seqüência das diagonais.
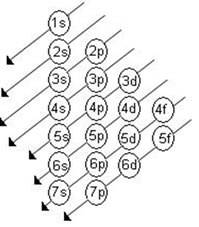
1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f, 6d
--------------------------------------------------------------------->
ordem crescente de energia
ordem crescente de energia
Onde cada número corresponde a uma camada eletrônica:
1=K
2=L
3=M
4=N
5=O
6=P
7=Q
Exemplo:
A camada de valência do As (arsênio), cujo número atômico é 33, é a camada N, pois é o último nível que contém elétrons.
A distribuição eletrônica deste átomo fica assim:
1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p3
O número 4 corresponde à camada N. O subnível p da camada N, neste caso não está completo, pois sobraram apenas 3 elétrons para este subnível. A camada N, neste caso formada pelos subníveis s e p, soma um total de 5 elétrons. Quando completa, esta camada (N) comporta até 32 elétrons, pois é formada pelos subníveis s, p, d e f.
Distribuição Eletrônica em Íons
Átomo: nº de prótons = nº de elétrons
Íon: nº de prótons (p) ≠ nº de elétrons
Íon positivo (cátion): nº de p > nº de elétrons
Íon negativo (ânion): nº de p < nº de elétrons
Distribuição Eletrônica em Cátion
Retirar os elétrons mais externos do átomo correspondente. Exemplo:
Ferro (Fe) Z = 26 → 1s2 2s2 2p6 3s2 3p6 4s2 3d6 (estado fundamental = neutro)
Fe2+ → 1s2 2s2 2p6 3s2 3p6 3d6 (estado iônico). Em estado de cátion, este átomo tem 2 elétrons a menos, ou seja, duas cargas negativas a menos. Isso significa que ele se torna positivo.
Distribuição Eletrônica em Ânion
Colocar os elétrons no subnível incompleto. Exemplo:
Oxigênio (O) Z = 8 → 1s2 2s2 2p4 (estado fundamental = neutro)
O2- → 1s2 2s2 2p6 (estado iônico). Em estado de ânion, este átomo recebeu 2 elétrons, ou seja, tem duas cargas negativas a mais. Isso significa que ele se torna negativo.
Átomo: nº de prótons = nº de elétrons
Íon: nº de prótons (p) ≠ nº de elétrons
Íon positivo (cátion): nº de p > nº de elétrons
Íon negativo (ânion): nº de p < nº de elétrons
Distribuição Eletrônica em Cátion
Retirar os elétrons mais externos do átomo correspondente. Exemplo:
Ferro (Fe) Z = 26 → 1s2 2s2 2p6 3s2 3p6 4s2 3d6 (estado fundamental = neutro)
Fe2+ → 1s2 2s2 2p6 3s2 3p6 3d6 (estado iônico). Em estado de cátion, este átomo tem 2 elétrons a menos, ou seja, duas cargas negativas a menos. Isso significa que ele se torna positivo.
Distribuição Eletrônica em Ânion
Colocar os elétrons no subnível incompleto. Exemplo:
Oxigênio (O) Z = 8 → 1s2 2s2 2p4 (estado fundamental = neutro)
O2- → 1s2 2s2 2p6 (estado iônico). Em estado de ânion, este átomo recebeu 2 elétrons, ou seja, tem duas cargas negativas a mais. Isso significa que ele se torna negativo.
Exemplos de distribuição eletrônica:
1 - Distribuir os elétrons do átomo normal de manganês (Z=25) em ordem de camada.
Solução:
Se Z=25 isto significa que no átomo normal de manganês há 25 elétrons. Aplicando o diagrama de Pauling, teremos:
K - 1s2
L - 2s2 2p6
M - 3s2 3p6 3d5
N - 4s2 4p 4d 4f
O - 5s 5p 5d 5f
P - 6s 6p 6d
Q - 7s 7p
Resposta: K=2; L=8; M=13; N=2
2 - Distribuir os elétrons do átomo normal de xenônio (Z=54) em ordem de camada.
Solução:
K - 1s2
L - 2s2 2p6
M- 3s2 3p6 3d10
N- 4s2 4p6 4d10 4f
O- 5s2 5p6 5d 5f
P- 6s 6p 6d
Q- 7s 7p
Resposta: K=2; L=8; M=18; N=18; O=8
1 - Distribuir os elétrons do átomo normal de manganês (Z=25) em ordem de camada.
Solução:
Se Z=25 isto significa que no átomo normal de manganês há 25 elétrons. Aplicando o diagrama de Pauling, teremos:
K - 1s2
L - 2s2 2p6
M - 3s2 3p6 3d5
N - 4s2 4p 4d 4f
O - 5s 5p 5d 5f
P - 6s 6p 6d
Q - 7s 7p
Resposta: K=2; L=8; M=13; N=2
2 - Distribuir os elétrons do átomo normal de xenônio (Z=54) em ordem de camada.
Solução:
K - 1s2
L - 2s2 2p6
M- 3s2 3p6 3d10
N- 4s2 4p6 4d10 4f
O- 5s2 5p6 5d 5f
P- 6s 6p 6d
Q- 7s 7p
Resposta: K=2; L=8; M=18; N=18; O=8
Desafio:
Na tabela periódica dos elementos, o grupo A está disposto em ordem crescente (1.A, 2.A, 3.A, 4.A, 5.A, 6.A, 7.A e 8.A), por que o grupo B não está em disposto ordem crescente?
Resposta:
Porque no grupo B estão os elementos de transição, exemplo:
| 21Sc | - 1s2, 2s2, 2p6, 3s2, 3p6, 4s2, 3d1 => 1+ | Elemento eletropositivo. |
| 22T | - 1s2, 2s2, 2p6, 3s2, 3p6, 4s2, 3d2 => 2+ | Elemento eletropositvo. |
| 23V | - 1s2, 2s2, 2p6, 3s2, 3p6, 4s2, 3d3 => 3+ | Elemento eletropositivo. |
| 24Cr | - 1s2, 2s2, 2p6, 3s2, 3p6, 4s2, 3d4 => 4+ | Elemento eletropositivo/eletronegativo. |
| 25Mn | - 1s2, 2s2, 2p6, 3s2, 3p6, 4s2, 3d5 => 3- | Elemento eletronegativo. |
| 26Fe | - 1s2, 2s2, 2p6, 3s2, 3p6, 4s2, 3d6 => 2- | Elemento eletronegativo. |
| 27Co | - 1s2, 2s2, 2p6, 3s2, 3p6, 4s2, 3d7 => 1- | Elemento eletronegativo. |
| 28Ni | - 1s2, 2s2, 2p6, 3s2, 3p6, 4s2, 3d8 => 0 | Elemento neutro. |
| 29Cu | - 1s2, 2s2, 2p6, 3s2, 3p6, 4s2, 3d9 => 1+ | Elemento eletropositivo. |
| 30Zn | - 1s2, 2s2, 2p6, 3s2, 3p6, 4s2, 3d10 => 2+ | Elemento eletropositivo. |
Observação:
Sabe-se que:
IIIB = > d1, IVB => d2, VB => d3, VI => d4, VII = >; d5, VIII => d6, d7 e d8, IB = > d9 e IIB =>d10.
Por que ele agrupa a coluna do ferro (Fe), do cobalto (Co) e do níquel (Ni) como VIIIB?
Resposta:
Porque pertencem ao grupo de transição.
Desvendando a Matemática - Resolvendo Equações de 2º Grau Incompletas
Como resolver equações do 2º grau incompletas

Para resolver uma equação, que significa determinar o conjunto de soluções dessa equação.
Baseado nas condições acima, verificaremos como resolver as equações incompletas do 2º grau.
Ler Mais

Para resolver uma equação, que significa determinar o conjunto de soluções dessa equação.
Baseado nas condições acima, verificaremos como resolver as equações incompletas do 2º grau.
1º caso:
A equação é da forma ax2 + bx = 0, onde c = 0.
Resolva as seguintes equações incompletas do 2º grau, sendo U = R
Exemplos:
a) x2 – 4x = 0
Colocando o fator x em evidência, temos:
x. (x – 4) = 0
As raízes das equações são:
x = 0
x – 4 = 0
x = 4
Logo S = {0,4}
b) y2 + 10y = 0
Colocando o fator y em evidência, temos:
y.(y + 10) = 0
As raízes das equações são:
y = 0
y + 10 = 0
y = -10
Logo S = {0, -10}
Observe que nos exemplos acima, sempre procuramos colocar a variável em evidência para a equação seja solucionada mais rapidamente.
2º caso
A equação é da forma ax2 + c = 0, onde b = 0.
Resolva as seguintes equações incompletas do 2º grau, sendo U = R
a) x2 – 49 = 0
Calculando o termo independente e transpondo e termo, temos o seguinte:
x2 – 49 = 0
x2 = 49
x = +/- raiz quadrada de 49 (√49) – relação fundamental
x = +/- 7 ---à Raiz quadrada de 49 pertence R e é exata : 7
x = + 7 ou x = -7
S = {-7, 7}
b) 4x2 – 36 = 0
Calculando o termo independente e transpondo e termo, temos o seguinte:
4x2 = 36
x2 = 36/4
x2 = 9
x = +/- raiz quadrada de 9 (√9) – relação fundamental
x = + 3 ou x = -3
S = {-3, 3}
Desvendando a Matemática - Equação de 2º Grau
2x + 1 = 0, o expoente da incógnita x é igual a 1. Dessa forma, essa equação é classificada como do 1º grau.
2x² + 2x + 6 = 0
x³ – x² + 2x – 4 = 0
Assinar:
Postagens (Atom)
Prof. Jackson Dória | by TNB ©2010























